![]()
Probability is a way of summarizing the uncertainty of statements or events. It gives a numerical measure for the degree of certainty (or degree of uncertainty) of the occurrence of an event.
Another way to define probability is the ratio of the number of favorable outcomes to the total number of all possible outcomes. The enumeration of all possible outcomes is called as the sample space.
If there are totally n possible outcomes in a sample space, S and m of those are favorable for an event, A. then probability of event, A is given as
P(A) = (number of favorable outcomes) / (total number of possible outcomes)
= n(A) / n(S)
= m/n
Example:- Find the probability of getting a 3 or 5 while throwing a dice.
Answer:- Sample space, S = {1,2,3,4,5,6} and Event, A = {3,5}.
n(A) = 2 and n(S) = 6.
So, P(A) = n(A) / n(S) = 2/6 = 0.3333
All probability values are positive numbers not greater than 1, i.e. 0 ≤ p ≤ 1. An event that is not likely to occur or impossible has probability zero, while an highly likely event has a probability one.
Example:- P(A pregnant human being a female) = 1
Example:- P(A human male being pregnant) = 0.
If the probability that an event occurs is p, then the probability that the event does not occur is q = (1-p). i.e. probability of the complement of an event = 1 - probability of the event.
i.e. P(Ā) = 1 - P(A)
Example:- Find the probability of not getting a 3 or 5 while throwing a dice.
Answer:- Sample space, S = {1,2,3,4,5,6} and Event, B = {1,2,4,6}.
n(B) = 4 and n(S) = 6.
So, P(B) = n(B) / n(S) = 4/6 = 0.6667
Now A and B are complementary events, i.e. B = Ā.
So: 1 - P(A) = 1 - 0.3333 = 0.6667 = P(B) = P(Ā).
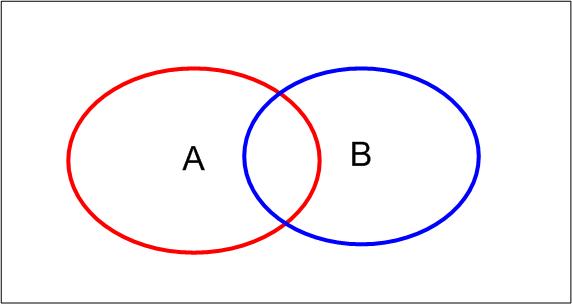
If A and b are two different events then, P(A U B) = P(A) + P(B) - P(A ∩ B). Consider the Venn diagram. P(A U B) is the probability of the sum of all sample points in A U B. Now P(A) + P(B) is the sum of probabilities of sample points in A and in B. Since we added up the sample points in (A ∩ B) twice, we need to subtract once to obtain the sum of probabilities in (A U B), which is P(A U B).
Example:- Probability that John passes a Math exam is 4/5 and that he passes a Chemistry exam is 5/6. If the probability that he passes both exams is 3/4, find the probability that he is pass at least one exam.
Answer:- Let M = John passes Math exam, and C = John passes Chemistry exam.
P(John passes at least one exam) = P(M U C) = P(M) + P(C) - P(M ∩ C)
= 4/5 + 5/6 - 3/4
= 53/60
If two events, A and B are mutually exclusive then, P(A U B) = P(A) + P(B). This follows immediately from (3). Since A and B are mutually exclusive, n(A ∩ B)=0 and so P(A ∩ B)=0.
Example:- What is the probability of getting a total of 7 or 11, when two dice are rolled.
Answer:- Let A be the event that the total is 7 and B be the event that it is 11.
Sample space, S = { (1,1), (1,2), .........., (2,1), (2,2), ........., (6,6) }
n(S) = 36.
A = { (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) } and n(A) = 6.
So P(A) = 6/36 = 1/6.
B = { (5,6), (6,5) } and n(A) = 2.
So P(B) = 2/36 = 1/18.
Since, we cannot have a total both 7 and 11, A and B are mutually exclusive.
i.e. (A ∩ B) = 0.
So we have P(A U B) = P(A) + P(B) = 1/6 + 1/18 = 2/9.
A person draws 5 cards from a shuffled pack of cards. Find the probability that the person has at least 3 aces. Find the probability that the person has at least 4 cards of the same suit.
Two cards are drawn from a pack, without replacement. What is the probability that both are greater than 2 and lesser than 8.
A permutation of the word "white" is chosen at random. Find the probability that it beings with a vowel. Also find the probability that it ends with a consonant.
A dice is tossed 5 times. Find the probability that we will have 4 of a kind.
Find the probability that a leap year will have 53 Sundays.
![]()